Lean Inventory Management in the Wood Products Industry: Examples and Applications
ID
420-148 (CNRE-132NP)
Introduction
One of the most difficult aspects of any manufacturing system is to control inventory. Keeping the right amount of inventory is not straightforward, so managers need to address the issue in a proper way. In wood products industries around the United States and in other countries, the problem seems to be the same: From lumber storage all the way to finished product, large quantities of inventory are piled up in the system.
Could this inventory accumulation be damaging performance? The simplest answer is from the point of view of “lean thinking.” Lean thinking is a philosophy that encourages the elimination or minimization of any form of waste. Excessive waste in a system adds costs to the final product and, most likely, customers are punished for the inefficiency.
One of the major sources of waste is the accumulation of inventory in your system. Not only is the money already paid for the inventory, but also for the holding cost involved. In the case of work in process (WIP) and finished inventory, you need to add other costs, such as labor and indirect costs, to the cost of raw materials.
Cost is not the only factor. With accumulated excess inventory, your lead times might be getting longer and your customers will have to wait longer for their products.
Either way you look at it, it makes sense to understand the basics of inventory control. This article will go through the basics using some real examples and applications in wood products industries.

How Important Is Inventory Control?
Inventory decisions are risky and they make a large impact throughout the supply chain (Bowersox, Closs, and Cooper 2021). Without proper planning, a manufacturing company can run out of raw material, negatively impacting the company and its customers. Likewise, overstocking of raw materials, work in process inventory, or finished goods could also hurt the company’s profitability. Wood products industries should carefully plan and manage inventory. There are some fundamental issues that need to be considered when planning inventory for wood products manufacturing firms.

- Raw materials are the first and foremost form of inventory. At a wood products manufacturing site, raw materials in multiple forms, including logs, lumber, composites, or chips, are transformed into higher value-added products. Wood products firms need to carefully design their warehouse or storage facilities for the special requirements of this biological raw material. In some locations, weather-related factors could affect log supply. To prevent “log starvation,” a company may employ a strategy of stockpiling that requires extra space, additional handling, proper identification of species and harvest date, and special care to prevent log degradation. Figure 1 shows an example of a log with extensive mechanical and biological damage that might have occurred from poor inventory management.
- In most wood products industries, the accumulation of inventory is more notorious in the form of work in process inventory. In most cases, WIP is used as a buffer to compensate for poor scheduling and production planning practices. It is important to mention that an excessive amount of WIP not only affects cycle time and throughput, but also the profitability of the company because WIP has by now absorbed raw material, labor, and overhead costs. Figure 2 shows WIP accumulation in a secondary wood products facility.
- Most wood products manufacturing firms work under the “make-to-stock” (MTS)1 strategy, because demand spurts and supply bottlenecks make “just-in-time” production unfeasible. Stocking excessive amounts of finished wood products such as lumber, plywood, veneer, OSB, MDF, I-joists, or furniture reduces profit because storage costs for these inventory goods are significantly more than the cost of raw materials or WIP inefficiencies due to greater costs already absorbed.
- The purchase price of raw materials is not the only cost to consider when planning inventory. In addition to the purchase price, there is also the cost of setting up an order and the cost of holding or maintaining inventory.
- Finally, you should provide the highest level of service to your company’s customers while maintaining the least possible amount of inventory in stock. The concept of inventory is strongly related to the lean-thinking philosophy. In a perfect “lean” world, inventory would not exist because it ties up cash and other resources. However, we have learned that in the wood products industry, inventory is needed to compensate for variability and uncertainty.
Therefore, inventory is unavoidable in order to balance against uncertainty — not just in the form of raw material, but also in the forms of WIP and finished goods.
As seen in the previous section, inventory planning involves the consideration of the three types of inventory (raw material, WIP, and finished goods), inventory cost issues, customer service rates, and process efficiency. Overall, the goal is to balance the need for inventory in every stage of the process against the uncertainty.
With this consideration in mind, the purpose of this article is to address the most fundamental question in inventory planning: How much should be ordered if we want to keep the company as process-efficient (lean) as possible and with the highest possible achievable customer service rates?
Important Definitions
The definition of a lean inventory policy requires clarification of certain terms. We define the following important terms that are necessary to accomplish our goal:
Setup cost: The cost associated with placing an order from a supplier. Every time an order needs to be placed, the company will spend some time and money placing it. Also, it might take more than one person to place an order, and lack of a well-planned ordering system can be very time-consuming and inefficient. Keep in mind that the more often orders are placed or replenished, the higher the total inventory costs. Counterintuitive to this consideration, the fewer orders placed, the more inventory will be needed to meet demand.
Holding cost: The cost associated with maintaining the inventory. Taxes, insurance premiums, obsolescence, storage space, handling, and information technology expenses are the most common financial aspects of holding costs.
Unit cost: The amount of money that is paid to purchase or create one unit of inventory.
Demand: The amount of units required in a certain time. It is usually expressed in units per day, units per month, or units per year, depending on the performance cycle a company might use.
Average inventory: Figure 3 shows how a simple inventory model works. This graph is also known as the saw-tooth plot. At time zero, an order of 10,000 board feet (BF) is placed with a local lumber supplier. In a perfect world, lumber will arrive instantly and be consumed uniformly for 30 days, at a rate of 333.33 BF per day. On day 30, a new order is placed for the same quantity and it arrives instantly on that day. The amount of lumber ordered every 30 days represents the order quantity or “Q.” The average inventory held is calculated as Q/2. In this case, the average inventory is 5,000 BF.
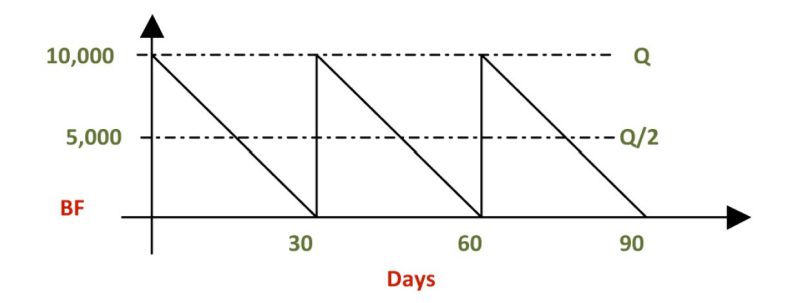
Service level rate: This is a performance measurement set by management that is closely linked with customer service. For example, if a lumber company has a service level rate of 95 percent, this indicates that, on average, 95 orders out of 100 will be filled and delivered on time. The other five orders are backlogged. As we will see later on, the higher the service level, the higher the associated inventory holding costs. Therefore, management should have a clear idea of how much it costs to offer a certain service level to its customers, compared to the cost of maintaining an order backlog.
Safety stock: A part of the total inventory that is used to protect the manufacturing system from starvation if the placed order fails to arrive on time. Safety stock works very well to protect against delivery variability — specifically, random demand. An inventory model that uses safety stock to prevent stockouts is more closely related to real world situations. Figure 4 shows an inventory model that uses safety stock as part of inventory policy.
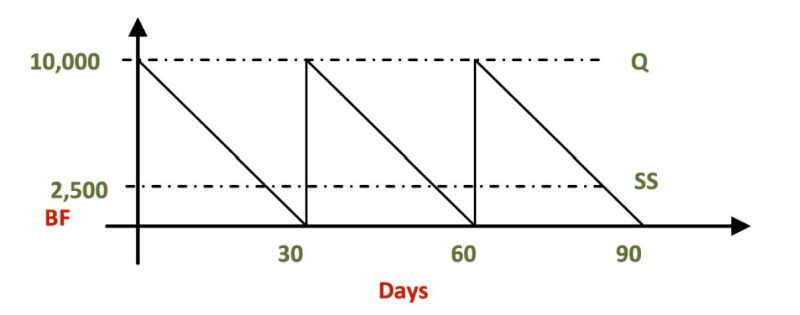
Similar to service level, the amount of safety stock is typically determined by management. A statistical procedure is sometimes used that considers historical demand variability and holding costs as part of the calculations.
Reorder point: Used as a trigger or flag to set up a new order. To calculate the reorder point (RP), the firm will need to know how much time it takes for its supplier to deliver a new order. Figure 5 illustrates the use of the reorder point.

For instance, assume that it takes 15 days for the supplier to deliver an order after it is placed. If the daily demand is 333 BF per day, in 15 days a total of 5,000 BF will be consumed. If the company wishes to keep a safety stock of 2,500 BF, as shown in figure 5, then new orders need to be placed when the inventory level reaches 7,500 BF. Mathematically, the reorder point can be expressed as
RP = (D x S) + SS, (1)
where
D = demand,
S = supplier lead time (days),
SS = safety stock.
How Much to Order?
Now that we have addressed the most important concepts in lean inventory planning, it is time to come back to the fundamental question: How much should be ordered to keep a minimum stock level without affecting customer service? To answer this question, we will use the inventory costs discussed above to develop an inventory model. Our solution will have to satisfy total minimum costs to be a feasible solution. There are three main cost components that make up the total inventory cost (TIC):
1. The unit cost is defined as
unit cost = DCu' (2)
where
D = demand,
Cu = cost of buying one unit.
2. The holding cost is given by the equation
holding cost = Ch (Q/2') (3)
where
Q/2 = average inventory,
Ch = cost of keeping or maintaining one unit in the warehouse.
3. The setup cost, Cs, is determined by the formula
setup cost = (D/Q) Cs' (4)
where
D = demand, usually expressed as yearly demand,
Q = the number of units ordered per order,
Cs = the cost of setting up one order.
Therefore, the TIC or incremental cost is given by the sum of the three cost components — equations (2), (3), and (4) — as shown in equation (5):
TIC = DCu + Ch (Q/2) + (D/Q) Cs' (5)
The relationships of the holding cost, setup cost, and total cost are shown in figure 6. In this graph, the green line represents the total incremental inventory cost (as in equation (5)), the red line represents the holding cost (equation (3)), the blue line is the setup cost (equation (4)), the horizontal axis is the number of units, and the vertical axis represents cost. Figure 6 shows that the holding cost (red line) increases as the number of units per order increases. Also, the setup cost (blue line) decreases if the number of units per order increases.
Note that the green line has a minimum (look for the lowest point in the plot). This will be the lowest or minimum cost. In figure 6, this point intersects with the horizontal axis at approximately 4,500 (see orange vertical line). This means that if an order of 4,500 units is placed during a time period it will yield the minimum possible cost. Any number of units below or above 4,500 will produce a higher total inventory cost.
This graphic example would be more helpful if we already knew how many orders (D/Q) need to placed over a time to achieve the minimum cost; however, we do not know that yet. So, how can we order Q units to keep the TIC at a minimum? Again, take a look at figure 6. To determine the quantity Q, examine the intersection point of the holding cost (red line) and the setup cost (blue line). The point intersects with the horizontal axis at approximately 4,500 as it does the lowest point of the TIC. If both curves (holding and setup costs) intersect at the same point as the TIC, they are equal. At this intersection point we have:
holding cost = setup cost
Using equations (3) and (4) results in
Ch (Q/2) = (D/Q) Cs' (6)
Solving for Q, we can find our economic order quantity (EOQ, or simply “Q”) that will minimize the TIC as shown in figure 6:
Q2 = (DCS 2)/Ch, (7)
and finally,
Q = √(DCs 2) / Ch , (8)
The final calculation of the EOQ equation (8) does not include the unit cost Cu, because quantity does not affect the TIC or incremental price. How can we explain this? Intuitively, we can say that ordering just one unit is the same cost of ordering 10,000 units. Mathematically, this can be shown if you take the first derivative of equation (5) for EOQ. Notice that the first term (unit cost) does not depend on EOQ; therefore, the derivative of a constant is zero.
Let’s take a closer look to the example shown in figure 6 to explain the EOQ concepts in action. This is the case of a small furniture manufacturer that produces high-end office furniture of several hardwood species. We will review the EOQ model for ordering walnut lumber. These are the initial parameters:
D = 50,000 BF per year,
Cu = $4.50 per BF,
Ch = $1.25 per BF,
Cs = $250 per order.

If we use equation (8), then we have
Q = √(DCs 2 / Ch) = √[(50,000 BF x $250/order x 2) / $1.25/BF] = 4,472.14 BF
This means that every order of walnut lumber should be of 4,473 BF (rounded up). This is the economic order quantity or EOQ. If you divide D by the EOQ, then you know you need to place 11.17 orders/year.
This procedure shows how much to order to keep
D/Q = (50,000 BF/year) / 4,473 BF = 11.17 orders/year
the total holding and setup costs to a minimum. The EOQ model is very important to establish the basic relationships in terms of cost and how much to order every time. However, the EOQ model relies on a few assumptions that are worth mentioning:
- Demand is constant.
- Lead time from supplier is known and constant.
- Orders are filled or replenished instantly.
- There is no in-transit inventory.
- Unit cost is independent of order quantity or time.
The next section will show us how to calculate an optimal quantity order when considering random demand. This new model is more closely related to a real-world situation, and it requires that the reader have some basic understanding of calculus and probability concepts. We will try to avoid as much calculus and probability as possible.
The Pencil Vendor Model: Dealing With Variability
This second inventory model will address the case where demand is random and there is a cost associated with ordering too much or ordering too little, using equations and the general model definition from Hopp and Spearman (2008).
To illustrate our second model, we will use a real example taken from a pencil manufacturing facility. The reason to choose this type of wood products industry is because it is a product that has cyclical demand.
This particular firm only manufactures pencils during a portion of the year in preparation for the start of the academic year. The company uses a raw material called gmelina (Gmelina arborea), a tropical hardwood that has a harvesting cycle of 10 years. Besides being a fast- growing species, gmelina pencils are easier to sharpen than other wood species. Figure 7 shows a picture of the pencil manufacturing site where this inventory model was applied in order to deal with random demand over a very short period of time.

First, let’s take a look at the cost issues. Remember that we will have to define our model starting with the total inventory cost or incremental cost as we did with the economic order quantity model.
If the EOQ estimate is short of the real demand, D, then profit is lost from a potential sale, or Cs. If production cost of one pencil is $0.10 and it sells for $0.20 and inventory is lagging, then a lost profit of Cs = $0.20 − $0.10 = $0.10 per unit is incurred. Conversely, if EOQ happens to be larger than your actual demand, then you are going to have tied up capital (money) sitting in excess inventory, or Co. As demand is cyclical, pencil overproduction for next year cannot be supported, so the additional pencils are sold as discounted products at $0.05 per unit, resulting in a loss per excess of inventory of Co = $0.10 − $0.05 = $0.05, which implies that it is less costly per unit to overproduce than to be short of actual demand. A lost sale costs $0.10 per unit, and an overage costs only $0.05 per unit.
The following formula is then used to create a new inventory model of units over:
units over = max{Q − D,0}
This implies that if Q is greater than or equal to D, then the overage is simply Q minus D, but if Q is less than D, then the overproduction is zero, meaning that there was actually a shortage of pencils instead of an overproduction. The following formula is used to estimate a shortage:
shortage = max{D − Q,0} .
This tells us that if D is greater than or equal to Q, then the actual shortage is D minus Q. Otherwise, there is overproduction, so the shortage is zero. Total inventory cost is determined by
TIC = C0 *max{Q − D,0} + Cs *max{D − Q,0}
Finding the value of Q that will minimize the TIC utilizes the same procedure as the previous model2. A plant engineer in the pencil manufacturing site found out that the demand, D, is equal to 1,300,450 units per year, with a standard deviation of σ = 155,210 pencils per year. With this information, we can calculate the value of EOQ as:
Q = Q* = µ + zσ
= 1,300,450 + 0.75 x 155,210
= 1,416,640 units.
This result tells us that the pencil manufacturing site needs to produce 0.7486 standard deviations above the average demand (1,300,450 pencils). The difference from this example to the previous one is that we have introduced demand variability, a closer approach to real- world scenarios than the case of deterministic demand.
Final Remarks
The complexity and variety of inventory models is broad. This paper presents the very basics of operations management literature on inventory planning covering two models: one that works with deterministic demand and one that works with random demand. They are both useful to start getting a grasp on how inventory
planning control can help a company be more profitable and customer-oriented. Both models have their strengths and weaknesses, but in general, they represent a variety of different mathematical solutions to the problem of inventory and how we can keep a company with just enough stock running (lean-oriented). Our objective
in this paper is to get you started, motivated, and concerned about why planning inventory is essential to both minimizing waste and increasing customer satisfaction.
References
Bowersox, D., D. Closs, and M. Cooper. 2021. Supply Chain Logistics Management. 4th ed. New York: McGraw-Hill.
Hopp, W., and M. Spearman. 2008. Factory Physics. 3rd ed. New York: McGraw-Hill.
Appendix: Technical Note for the Pencil Vendor Model
(Hopp and Spearman 2001)
Finding Economic Order Quantity to Minimize Total Inventory Cost
First we need to transform the TIC equation into a derivative so we can find the minimum. The new TIC formula will now look like this:
dTIC(Q) = C0 ∫Q0(Q – x)g(x)dx + Cs ∫∞Q (x – Q)g(x)dx.
To solve this derivative, Leibnitz’ rule is required but is not explained in this technical note. After taking the derivative and setting the result equal to zero, we have:
dTIC(Q) = C0 G(Q) – [1 – G(Q)] = 0.
which can also be expressed as:
TIC = C0Q − Cs[1 − Q] = 0.
Notice that TIC should equal zero to find the minimum TIC. Solving for EOQ, we have:
Q = Cs / (C0 + Cs) (9)
Random Demand
Note that according to equation (9), the economic order quantity for this model depends only on the cost of running out of stock or overstocking, as expected. As random demand (variability) comes into play, EOQ in equation (9) has to be defined for some probability distribution. If the demand, D, is equal to 1,300,450 pencils, normally distributed with a mean of µ and a standard deviation of σ = 155,210 pencils, and assumption of normality holds for the demand, then we can assume Q = (Q* − D)/σ is normally distributed also, with a mean3 of zero and standard deviation of one.
Therefore, we can use this result to express our EOQ as:
Q = ø [(Q* - µ) / σ] = z = [Cs / (C0 + Cs)] (10)
where z is the value in the standard normal table, and hence:
Q* = μ + zσ. (11)
So, in order to calculate the final value of EOQ, we need to first calculate the value of z. For this calculation, we will use equation (10):
z = $0.1v / ($0.05 + $0.1) = 0.67
By looking at a normal table, we can find that the value of Ф(0.67) = 0.7486. We need to do this because there is no possible way to express ø(z)=∫-∞z ø(y)dy as a simple, closed-form expression. These tables are included in any statistical and probability book or incorporated in scientific calculators or spreadsheets.
Now we can insert this value into equation (11) to obtain our final EOQ*:
Q*= μ + zσ = 1,300,450 + 0.7486 x 155,210 = 1,416,640 pencils
Notice that when demand is random, the economic order quantity depends on the probability distribution of the demand and the cost of overproducing or underproducing. Another important insight is that increasing the variability of the demand might increase or decrease the order quantity, depending on the values of Ф(z).
1. An inventory point where customers expect to be able to obtain parts or products without delay.
2. See appendix for technical note that explains how to find the value of Q for this example.
3. A measure of central tendency of a group of data.
Virginia Cooperative Extension materials are available for public use, reprint, or citation without further permission, provided the use includes credit to the author and to Virginia Cooperative Extension, Virginia Tech, and Virginia State University.
Virginia Cooperative Extension is a partnership of Virginia Tech, Virginia State University, the U.S. Department of Agriculture (USDA), and local governments, and is an equal opportunity employer. For the full non-discrimination statement, please visit ext.vt.edu/accessibility.
Publication Date
May 3, 2021



